关键词: 全国招教
初中《矩形》
1.题目:八年级《矩形》片段教学
2.内容:

3.基本要求:
(1)试讲约10分钟;
(2)引导学生进行小组讨论;
(3)结合教学内容,适当板书
教案
教学目标:
1.知道矩形的概念,掌握矩形特点。
2.经历思考,探究过程,发展总结归纳能力,体验数形之间联系,逐步学会利用数形结合思想分析解决有关思想。
3.积极参与数学活动,对其产生好奇心和求知欲,形成合作交流的学习习惯。
教学重点:理解矩形的概念。
教学难点:利用矩形的性质解决相关问题。
教学过程:
一、游戏活动,引入新课
如图,用6根火柴棒首尾相接摆成一个平行四边形。
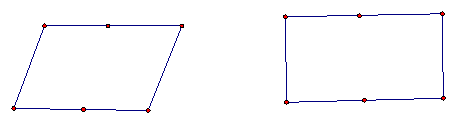
思考:(1)能摆成多少个不同的平行四边形?它们有什么共同的特点?(2)在这些平行四边形中,有没有面积最大的一个平行四边形?说出你的理由?(3)这个面积最大的平行四边形的内角有什么特点?量一量它的两条对角线的长度,你有什么发现?教师在学生回答的基础上,引入新课题。
二、合作探究,学习新知
1.矩形的概念
在上面“活动导入”和小学的知识基础上,引导学生归纳出矩形的概念:
有一角是直角的平行四边形是矩形;
让学生举出三个日常生活中的矩形的实例。
2.矩形的性质
根据上面的定义提问:
(1)矩形是不是平行四边形?
(2)平行四边形是不是矩形?
(3)平行四边形的性质矩形是不是也具备?
(4)矩形有没有与平行四边形不同的性质?
教师在学生回答的基础上,引导学生得出:矩形不但具备一般平行四边形的所有性质,还具备一般平行四边形没有的特殊性质:
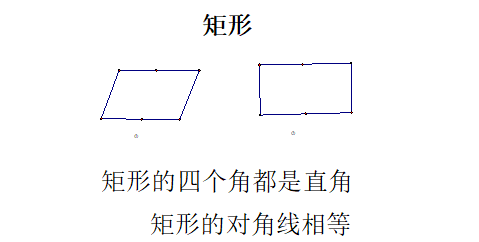
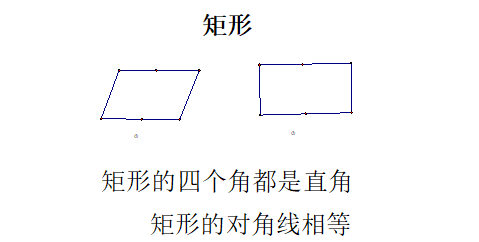
(1)矩形的四个角都是直角;
(2)矩形的对角线相等。
教师根据矩形的性质2,画出图形,写出已知、求证,让学生独立完成性质2的证明。
已知:如图,AC和BD是矩形ABCD的对角线;
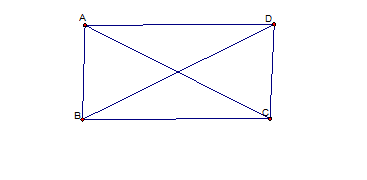
求证:AC=BD。
教师让学生独立完成证明过程,让一位学生板演,教师是学生完成证明过程后,进行点评指正。
3.讲解范例
已知:如图,在矩形ABCD中对角线AC、BD。
相交于点O,∠AOD=120°,AO=4cm。

教师在学生回答后让学生独立完成解题过程,让一位学生板演,教师最后进行点评指正。
4.矩形的对称性
教师根据例1,再通过作图的方式,说明矩形既是轴对称图形,又是中心对称图形,有两条对称轴。
三、巩固运用,实践创新
学生独立完成课本第96页的“练习”1、2两题,教师巡视指导,最后进行点评指正。
四、总结体会,反思提升
通过本节课的学习,你有哪些收获?鼓励学生畅所欲言,各抒己见。学生总结为主,引导学生从知识、方法、情感等方面小结本节课所学内容。老师辅助补充。
1.矩形不但具备一般平行四边形的所有性质,还具备一般平行四边形没有的特殊性质是:
(1)矩形的四个角都是直角;
(2)矩形的对角线相等。
2.矩形既是轴对称图形,又是中心对称图形,有两条对称轴。
五、课后作业,拓展延伸
1.基础作业:课后习题1-2;
2.开放性思考题:你能找出生活中的矩形图形并说说相应的性质吗?
六、板书设计
试讲逐字稿
一、游戏活动,引入新课
师:上课!同学们好,请坐!
师:各位同学,在刚刚上课之时,老师走进教室,看到有几位同学在讨论一道题目,老师把这道题目板书在黑板上给大家来分享一下。
师:这个题目就是现在有6根火柴棒,那么它可以拼成多少种不同的平行四边形呢?
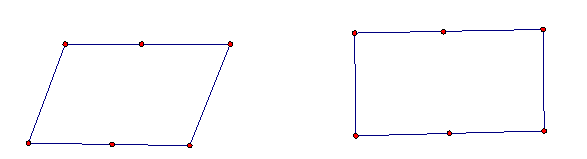
师:老师看到左边第二排的女生,你有想法!
生:嗯,请坐!她告诉老师,这6根火柴棒可以拼成任意多个平行四边形,因为平行四边形是具有不稳定性的,它可以进行任意的拉伸,那么这么多个平行四边形中,他们有什么共同点呢?诶,大家都告诉我了,说他们的底边相同,好,既然底边相同,老师就问大家了,这些平行四边形中,有没有哪个平行四边形面积是最大的?
师:好,老师看到右边这位男生,你来告诉老师。
师:嗯,思路很清晰,请坐!他说当这个平行四边形两条边,也就是两根火柴棒垂直的时候,它的面积是最大的,老师先把他的想法板书在黑板上。
师:大家看,为什么会觉得这两根火柴棒垂直的时候面积是最大的呀?噢,因为平行四边形的面积等于底乘高,刚刚在这么多个平行四边形中,由于底边是相等的,所以当这个火柴棒与底边垂直的时候,它的高度是最高的,因此面积也是最大的。
师:大家的反应都非常快,其实这一种特殊的平行四边形就是我们今天要学习的--矩形。
二、合作探究,学习新知
师:提到矩形,大家并不陌生,因为我们小学就已经学习过了长方形,那么现在大家结合我们以前所学习过的知识,和矩形的相关特点还有我们的教材,大家试着总结一下我们矩形的定义是什么,老师想找一个同学起来回答。
师:好!后排那位穿蓝衣服的男生,你来说。
师:嗯,语言非常精炼,请坐!他说:“有一个角是直角的平行四边形叫矩形。”老师再给大家重复一遍,有一个角是直角的平行四边形叫矩形。
师:这就是关于我们矩形的定义,好,那既然知道了我们矩形的定义以后,老师就有问题想问大家了,那矩形,首先它是一个平行四边形吧,那么,它具不具备我们平行四边形的性质呢?嗯,大家都在点头,因为它既然是特殊的平行四边形,自然就具备我们平行四边形的性质对不对,那平行四边形的性质是什么呀?嗯,对边相等,平行,对角也是相等的,所以我们的矩形自然也具备这样的性质。那有没有是我们矩形具备而平行四边形不具备的性质呢?
师:我们可以来观察一下,我们刚刚说过了,矩形是有一个角是直角的平行四边形,既然有一个角是直角,老师问大家,由于平行四边形对角相等,那它相对的这个角是不是也是直角啊,好,既然相对的角是直角,那么根据平行线的关系,所以它的同旁内角,嗯,也是直角,因为同旁内角是互补的,这就告诉我们了,矩形的四个内角都是什么呀?嗯,都是直角。
师:好,接下来,老师又有下面一个问题了,现在大家在纸上画一个矩形,将矩形的两条对角线连接起来,大家试着自己证明一下,矩形的对角线又有什么关系呢,现在同桌之间2人为一小组,老师给大家5分钟的时间,开始。
师:好,老师看大家讨论的差不多了,有没有哪位同学可以告诉老师的,好,课代表,你来给老师说一下。
师:嗯,慢一点,老师根据你的思路一点点的来复述,很好,在三角形ABC和三角形BCD中,嗯,由于两条对边是相等的,一条公共边,还有两个角是直角,所以根据边角边,我们可以证明两个三角形是全等的,既然两个三角形全等,所以两条对角线是相等的,非常棒,请坐!
师:课代表的想法大家都同意吗?嗯,大家都同意,其实这就说明了我们矩形的第二个性质,也就是我们矩形的对角线是相等的。
三、巩固运用,实践创新
师:好,这就是关于我们矩形的两条性质,大家都清楚了没有,那现在老师想考一考大家,大家看大屏幕,大屏幕上就是一个矩形,现在矩形ABCD,对角线AC、BD相交于点O,题目告诉我们∠AOD=120°,AO=4cm,第一问问△AOB的形状,第二问对角线的长度是多少,大家先动手在纸上试一下。
已知:如图,在矩形ABCD中对角线AC、BD。
相交于点O,∠AOD=120°,AO=4cm。
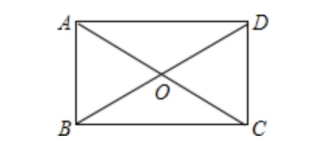
(1)判断△AOB的形状;
(2)求对角线的长。
师:好,老师看到班长举手最快你来告诉我们,嗯,慢一点,同样老师给你复述下,很好,由于平行四边形平行线的性质,我们首先可以证明△AOD和△BOC是全等的,所以两条对接线是互相平分的,又由于矩形的对角线又相等,所以AO=BO,首先我们可以判断它是一个等腰三角形,嗯,另外∠AOD=120°所以∠AOB=60°那么有一个角是60°的等腰三角形是等边三角形,很好哈,应用的非常不错。
师:那第二问呢,嗯,第二问就迎刃而解了,由于它是等边三角形,所以对角线的一半是4cm,对角线的长度自然就是8cm,非常棒。
四、总结体会,反思提升
师:好,那说明大家掌握的都非常不错了,各位同学,我们来一起回顾一下,这节课我们学习了关于矩形的相关性质,它的四个角都是直角,两条对角线是相等的。
五、课后作业,拓展延伸
师:那么大家回去以后可以在生活中看一下有没有一些相关的矩形,大家可以动手画一下它的对角线,去验证一下,下节课来与老师一起分享。
六、板书设计
答辩
1.矩形的性质以及判定方法有哪些?
【参考答案】
矩形的性质如下:
(1)矩形是特殊的平行四边形,因此矩形也是中心对称图形。
(2)矩形是轴对称图形,它有两条对称轴。
(3)矩形是特殊的平行四边形,因此具备所有平行四边形所具备的性质,可以把矩形的性质归结为如下三个方面:从边看,矩形对边平行且相等;从角看,矩形四个角都是直角;从对角线看,矩形的两条对角线相等且平分。
矩形的判定方法有如下几个方面:
(1)有一个角是直角的平行四边形是矩形。
(2)对角线相等的平行四边形是矩形。
(3)有三个角是直角的四边形是矩形。
(4)定理:经过证明,在一个平面内,任意两角是直角,任意一组对边相等的四边形是矩形。
(5)对角线相等且互相平分的四边形是矩形。
2.本节课的教学目标是什么?
【参考答案】
矩形这堂课,是基于学生之前已经学习过了平行四边形的相关概念及性质继续学习的,同时,学完本节课以后,也会后续学习正方形的相关概念及性质打下坚实的基础,因此,矩形这堂课在平行四边形整个模块中起到了一个承上启下的过渡作用。因此对于本节课的教学,我们需要继续渗透转化和推理的思维,帮助学生结合之前学习过的平行四边形的相关概念及性质,继续类比学习矩形的相关概念及性质,同时本阶段的学生好奇心强,初步具备了抽象逻辑思维,但是抽象思维尚不具体,也不足够,这都是我们在教学中需要考虑的因素。基于此,本节课的教学目标有如下三个方面:
(1)学生能初步理解矩形的概念,掌握矩形的两个性质,能应用矩形的性质解决生活中的简单问题
(2)学生经历动手操作、实践、证明等,感悟数学渗透、转化、从特殊到一般的思想,同时学生的组织能力、语言表达能力和动手操作能力得到培养。
(3)学生能感受到数学来源于生活,并服务于生活,体验到成功的快乐。

2024年教师招聘官方微信客服
手机微信扫描左侧二维码,添加客服老师微信领取
相关推荐:
手机登录下载
微信扫码下载
微信扫一扫,即可下载